|
|
Fr:Utiliser le Solver
From NeoWiki
Le Solver est un outil permettant de calculer les conditions qui réalisent la maximisation d'objecÂtifs et la minimisation de coûts en respectant des contraintes. Il peut résoudre des problèmes liÂnéaires ou non, mais il faut garder à l'esprit que les problèmes non linéaires sont beaucoup plus difÂficiles à résoudre. L'exemple suivant illustre l'utilisation de la fonction Solver dans le module Calc.
N.B. L'interface du Solver n'est pas localisée. Tout le texte est en anglais. Vous trouverez en bas de cette page un lexique traduisant les termes utilisés dans les fenêtres de dialogue, ainsi qu'une explication succinte de leur signification.
Contents |
Présentation du Problème
Supposons qu'une usine fabrique trois types de machines, A1, A2, A3. On désigne par pi le prix des matières premières et par hi le nombre d'heures de travail nécessaires à la fabrication d'une machine de type Ai. Le bénéfice par machine de type Ai est égal à bi.
Les variables d'ajustement sont les nombres xi de machines de type Ai fabriquées.
On cherche à calculer les valeurs des nombres xi qui rendent maximum le bénéfice total réalisé.
Ces données sont soumises à des contraintes, par exemple :
- chaque nombre xi doit être un entier. On veut fabriquer au moins 30 machines de chaque type.
- le coût total des matières premières doit être inférieur ou égal à 10 000 €
- le nombre total d'heures de travail doit être inférieur ou égal à 5 200.
| Machines | A1 | A2 | A3 |
|---|---|---|---|
| Nombre de machines | x1 | x2 | x3 |
| Prix des matières premières par machine | p1 | p2 | p3 |
| Nombre d'heures de travail par machine | h1 | h2 | h3 |
| Bénéfice par machine | b1 | b2 | b3 |
| Bénéfice à maxiÂmiser | b1x1+b2x2+b3x3 | ||
| Contraintes | x1 >= 30, x2 >= 30, x3 >= 30 | p1x1+p2x2+p3x3 <= 10 000 | h1x1+h2x2+h3x3 <= 5 200 |
Résolution du Problème
- Ouvrez un document Calc
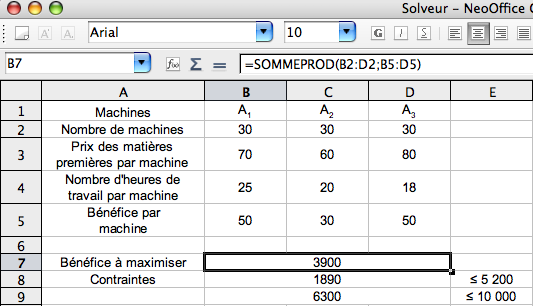
- Dans la feuille de calcul, entrez les données, comme le montre le tableau ci-dessous :
La valeur 1890 contenue dans la cellule B8 est la somme des heures de travail nécessaires à la fabrication de 30 machines de chaque type, soit SOMMEPROD(B2:D2;B4:D4).
La valeur 6300 contenue dans la cellule B9 est le coût des matières premières nécessaires pour produire 30 machines de chaque type, soit SOMMEPROD(B2:D2;B3:D3).
On doit rendre maximum le bénéfice total : SOMMEPROD(B2:D2;B5:D5)
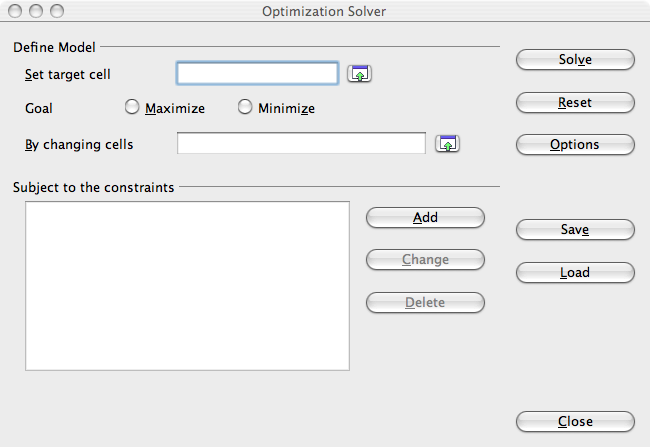
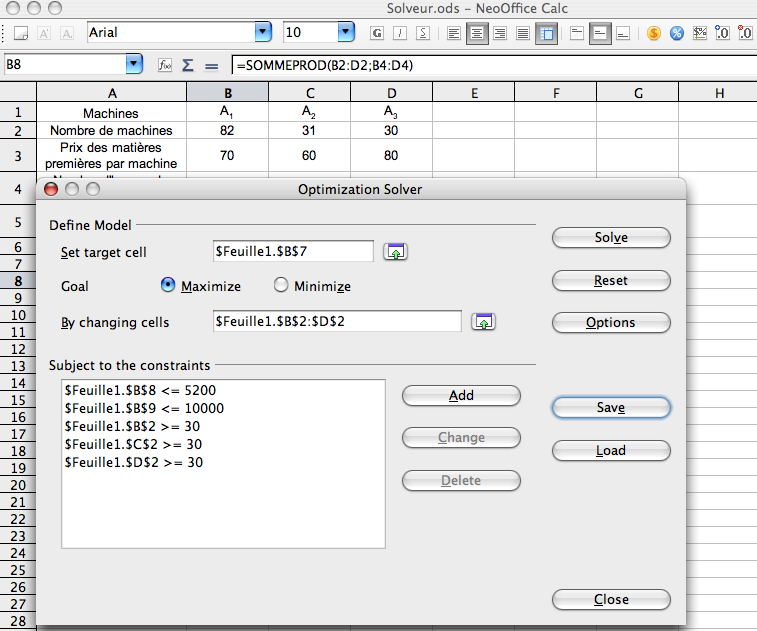
- Choisissez le menu Outils > Solver…. La fenêtre Optimization Solver s'ouvre.
- Définissez le modèle :
- N.B Toutes les références sont automatiquement traduites en références absolues par le solveur. Cela explique la présence du préfixe "$" dans les adresses des cellules.
- Cliquez sur la petite flèche verte à droite du champ Set target cell, puis cliquez sur la cellule contenant la fonction à optimiser, ici B7 contenant la formule donnant le bénéfice total. Cliquez de nouveau sur la flèche à droite du champ de saisie, la valeur $Feuille1.$B$7 est inscrite automatiquement dans le champ Set target cell.
- Cliquez sur Maximize. C'est le but à assigner.
- Cliquez sur la petite flèche verte à droite du champ By changing cells pour choiÂsir les cellules contenant les variables dont on veut déterminer les valeurs permettant de rendre le bénéfice maximum. Sélectionnez les trois cellules B2, C2, D2 en faisant glisser le curseur. Cliquez de nouveau sur la flèche à droite du champ de saisie. La plage $Feuille1.$B$2:$D$2 est inscrite auÂtomatiquement dans le champ By changing cells.
- Définissez les contraintes :
- Fixons les contraintes suivantes :
- SOMMEPROD(B2:D2;B4:D4) ≤ 5 200
- SOMMEPROD(B2:D2;B3:D3) ≤ 10 000
- B2 ≥ 30
- C2 ≥ 30
- D2 ≥ 30
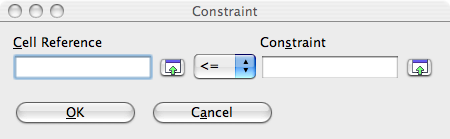
- Cliquez sur le bouton Add. La fenêtre Constraint s'ouvre.
- Cliquez sur la petite flèche verte à droite du champ Cell reference et cliquez sur la cellule B8, puis de nouveau sur la flèche.
- Dans le champ Constraint entrez la valeur choisie 5200.
- Cliquez sur OK.
- Cliquez de nouveau sur le bouton Add et ajoutez les quatre autres contraintes de la même manière. Changez le signe "<=" en ">=" pour les contraintes imposées aux valeurs xi.
- Fixons les contraintes suivantes :
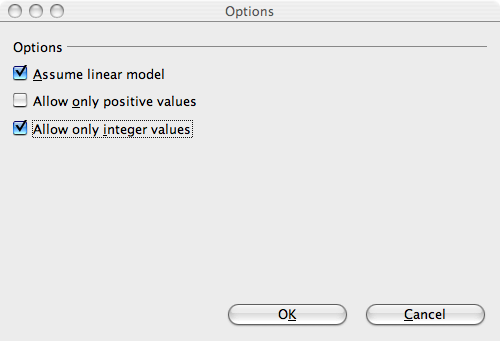
- Choisissez les options :
- Cliquez sur le bouton Options
- Dans la fenêtre Options qui s'ouvre, laissez cochée l'option par défaut Assume linear model et cochez l'option Allow only integer values.
- Cliquez sur OK.
- Cliquez sur le bouton Options
- Cliquez sur le bouton Solve.
- Le message Solution found apparait dans une boîte de dialogue. Cliquez sur OK.
- Les valeurs des cellules B2 à D2 ont été modifiées de sorte que le bénéfice soit maximum, dans les conditions fixées par les contraintes.
- Dans cet exemple, on obtient x1= 82, x2 = 31 et x3 = 30.
- Les valeurs des cellules B2 à D2 ont été modifiées de sorte que le bénéfice soit maximum, dans les conditions fixées par les contraintes.
- Vous pouvez enregistrer ce modèle en cliquant sur le bouton Save. En cliquant sur le bouton Load vous pourrez l'afficher ultérieurement et, par exemple, modifier les valeurs des contraintes ou des coûts de fabrication.
Lexique
| Fenêtre principale |
|---|
| Anglais | Français | Description |
|---|---|---|
| Define model | Définition du modèle | |
| Set target cell | Définition de la cellule cible | Adresse de la cellule contenant la mesure à optimiser |
| Goal | But | Définition de l'optimisation : maximiser ou minimiser |
| By changing cells | En modifiant les cellules | Plage de cellules contenant les valeurs qui seront modifiées |
| Subject to the constraints | Contraintes à respecter | Définition des conditions à remplir par les variables |
| Add | Ajouter | Ajoute une nouvelle contrainte |
| Change | Modifier | Modifie la définition de la contrainte sélectionnée |
| Delete | Supprimer | Supprime la contrainte sélectionnée |
| Solve | Résoudre | Lance le processus |
| Reset | Initialiser | Supprime toutes les valeurs entrées |
| Options | Options | Ouvre la fenêtre de dialogue Options |
| Save | Enregistrer | Enregistre les valeurs courantes dans les métadonnées du document |
| Load | Importer | Importe les valeurs enregistrées dans les métadonnées du document |
| Close | Fermer |
| Fenêtres Contraintes et Options |
|---|
| Anglais | Français | Description |
|---|---|---|
| Cell Reference | Adresse de la cellule | Permet d'entrer la référence de la cellule qui devra remplir la condition imposée |
| Constraint | Contrainte | Permet d'entrer la condition imposée qui peut être une valeur numérique ou la référence d'une cellule |
| Assume linear model | Modèle linéaire | Si cette option est cochée le solver utilise un algorithme de programmation linéaire, sinon il utilise un algorithme non-linéaire |
| Allow only positive values | Valeurs positives uniquement | Les variables de décision ne peuvent prendre que des valeurs positives |
| Allow only integer values | Valeurs entières uniquement | Les variables de décision ne peuvent prendre que des valeurs entières |
Lien
[Description du Solver] [en anglais]